Two-Party Popular Vote Forecast

For my two-party popular vote model, I used a similar set of predictors that I’ve used in previous blogs before:

• Polling Averages
  • Average of all polls from FiveThirtyEight From June to November
  • I took an average of polls closer to the election because of evidence that polls get better as they approach Election Day and to reduce one pollster from having a large influence on the predictor.
• A Measure of the Previous Election
  • Two-party popular vote from the previous presidential election
  • Results from the previous election, especially if a candidate is an incumbent, proved to be useful in predicting the result from this election.
• Incumbency
  • Is the candidate part of the incumbent party?
  • I chose to use incumbent party over incumbent candidate after testing both predictors in my model. The incumbent party variable yielded better results.
• Economic Measure
  • Presidential Job Approval Average from Gallup
  • I chose not to use GDP as my economic predictor because the COVID-19 pandemic has caused the GDP to swing wildly during 2020. Instead, I found that presidential job approval remained relatively steady and provided better results in my model. The averages are for each election year from January to November.
• Interaction between Incumbent Party and Presidential Job Approval
  • The interaction variable between incumbency and job approval makes sense because voters might reward the incumbent candidate more than the challenger if the job approval was high. The opposite might also be true where an incumbent is punished if the job approval was low.
• Party
  • The party of the candidate
  • The party acts as a control variable for my models.

I created 5 test models using a combination of these measures to see which model was the best. The results can be seen in the table below:

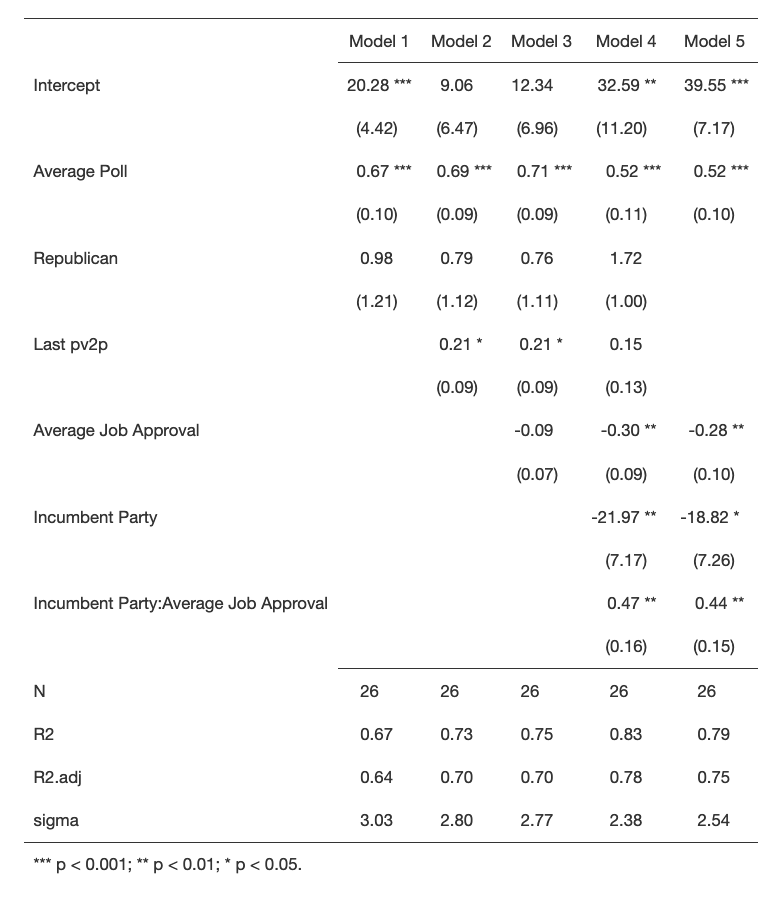
Focusing on the adjusted R-squared values at the bottom of the table, we can see that model 4 yields slightly better results in my in-sample testing with the highest adjusted R-squared of 0.78 and sigma of 2.38. In my out-of-sample testing, I used leave-one-out cross-validation and saw that model 4 had the lowest rmse value of 2.87. An interesting observation is that during my out-of-sample testing, model 2 and model 5 both performed similarly - just slightly worse than model 4 with a rmse of 2.96. However, our in-sample adjusted R-Squared value has model 5 performing much better than model 3. This shows the importance of using out-of-sample testing to evaluate models and not just in-sample testing.

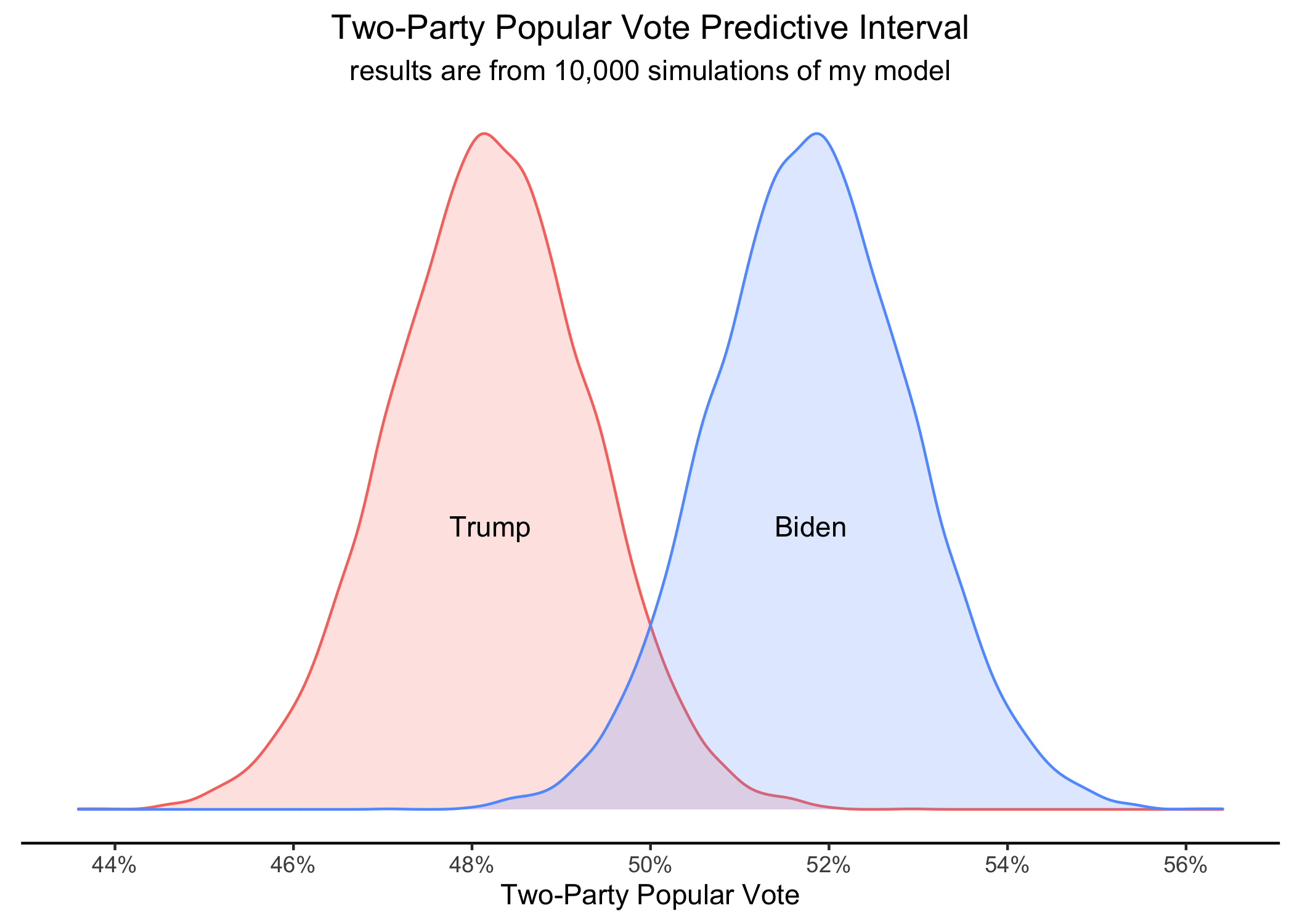
So, I used model 4 to forecast the two-party popular vote and ran 10,000 simulations. The predictive interval can be seen in this plot, where Biden won about 52% plus or minus 2% of the two-party popular vote in the simulated elections. Trump, on the other hand, won about 48% plus or minus 2%. Interestingly, Trump only won a greater share of the two-party popular vote in 517 of the simulated elections. So, Biden won the two-party popular vote in about 95% of the simulations. In the 2020 Election, I forecast that Biden has a better chance of winning the two-party popular vote than Trump at 52-48 with a margin-of-error of plus or minus 2.

Electoral College Forecast

For my state electoral college models, I used the same set of factors that I used for my national models. However, instead of using the previous election two-party popular vote to account for the previous election, I used the voter eligible population and number of state votes in past elections to create binomial logistic regression models for each state and the District of Columbia. One thing to note is that I treated Nebraska and Maine as winner-take-all states in my models because there was not enough historical data on each district (Nebraska and Maine use a split electoral vote system).

I compared this model (model 3) with other models that only used fewer predictors (just average polling for model 1 and average polling + job approval for model 2). In my in-sample testing, model 3 had the lowest rmse scores across the states and DC. Model 3 had lowest rmse scores compared to the other two models in nearly every state by 0.05 at most (for the North Carolina models). But, other states like Hawaii saw nearly identical scores across the three models. In my out-of-sample testing, I conducted a leave-one-out validation on just 2016. It was difficult to repeat this on models for every election year given that I was creating models for each state. However, the 2016 test prediction incorrectly forecasted some of the key battleground states that tipped the election in favor of Trump in 2016: Florida, Michigan, Nevada, Pennsylvania, and Wisconsin. However, pollsters are aware of the reason that caused this in 2016 - under-counting white, non-college voters. So, many of them have adjusted their polling to account for this in 2020. If they adjusted correctly, this shouldn’t be an issue for the 2020 forecast.

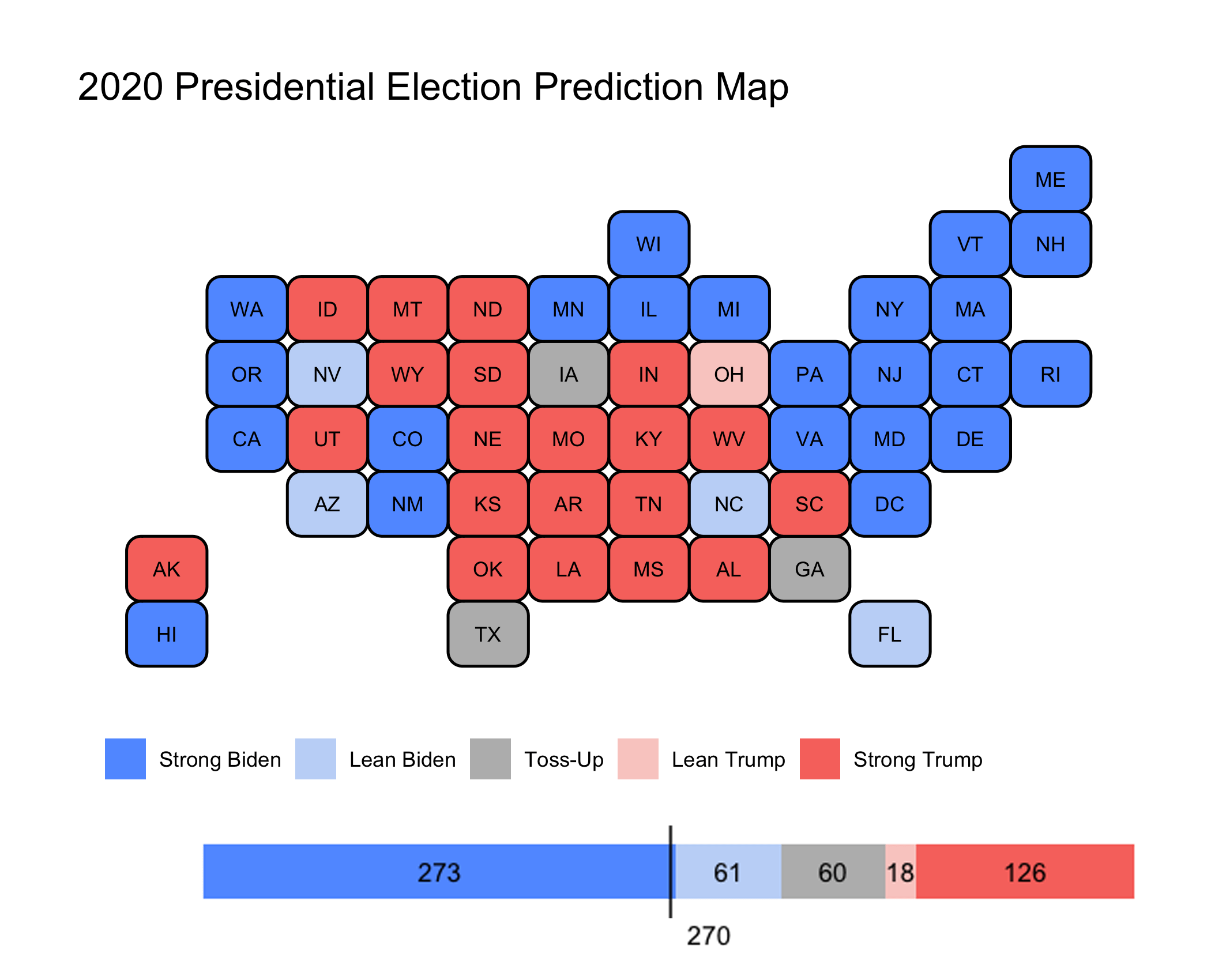
My 2020 electoral college forecast map is shown above. I define strong as a prediction that gives either candidate greater than a 5% margin-of-victory, lean as between 2-5%, and toss-up as any margin within 2%. Looking at the states that are considered toss-ups in my forecast, Texas and Iowa lean slightly in favor of Trump while Georgia leans slightly towards Biden. Texas has been a historically safe Republican state, however, Texas has already seen record-breaking early voting turnout - surpassing the total number of voters in 2016 already in early voting. So, it’d be interesting to see if Texas will flip Blue for the first time since 1976. The other two toss-up states: Georgia and Iowa are just as interesting. Georgia is also a historically red state, so it’d be interesting to see if it flips blue for the first time since 1992. Iowa flipped red in 2016, but went to Obama in 2008 and 2012. However, the latest poll from the Des Moines Register is favoring Trump.

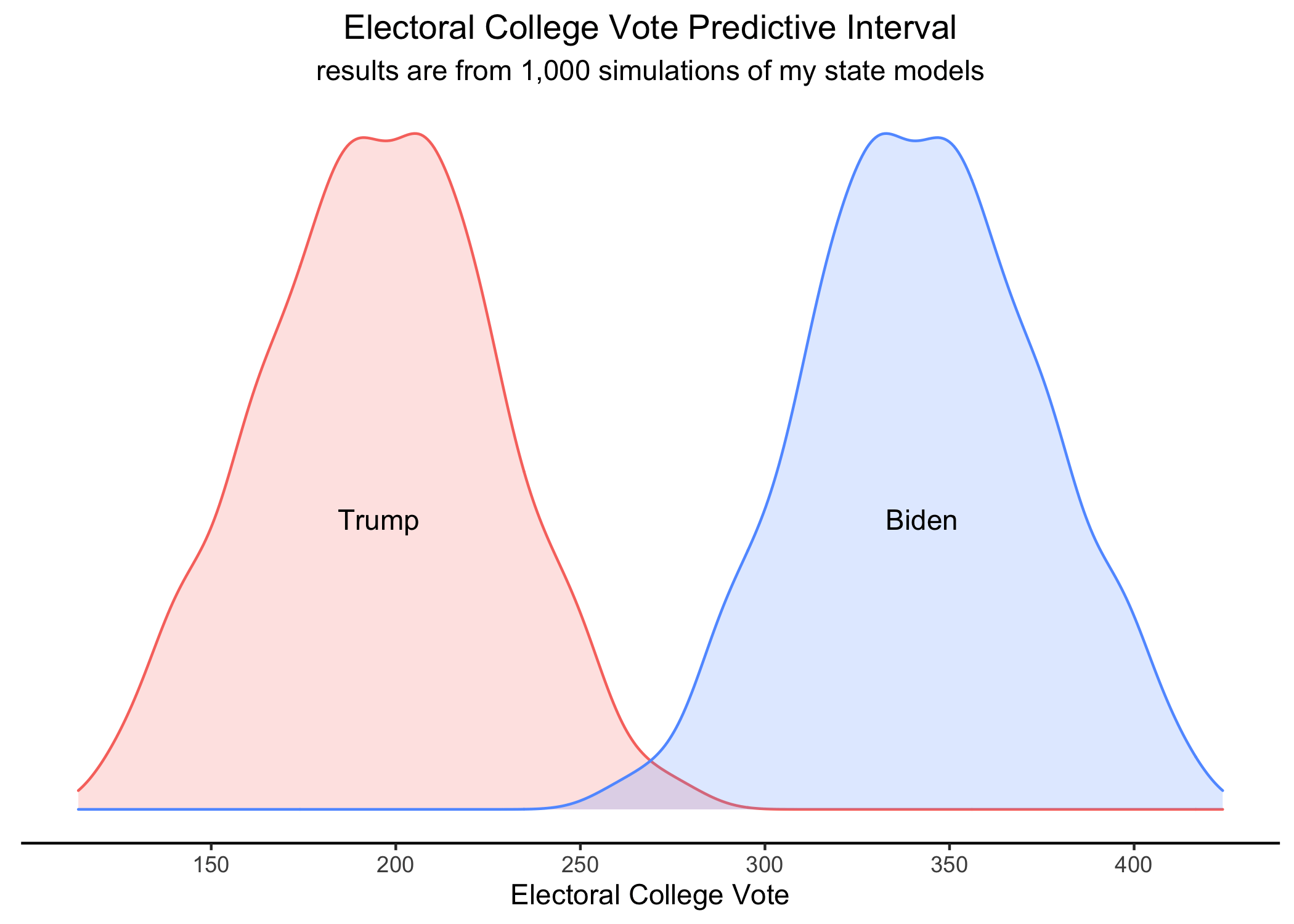
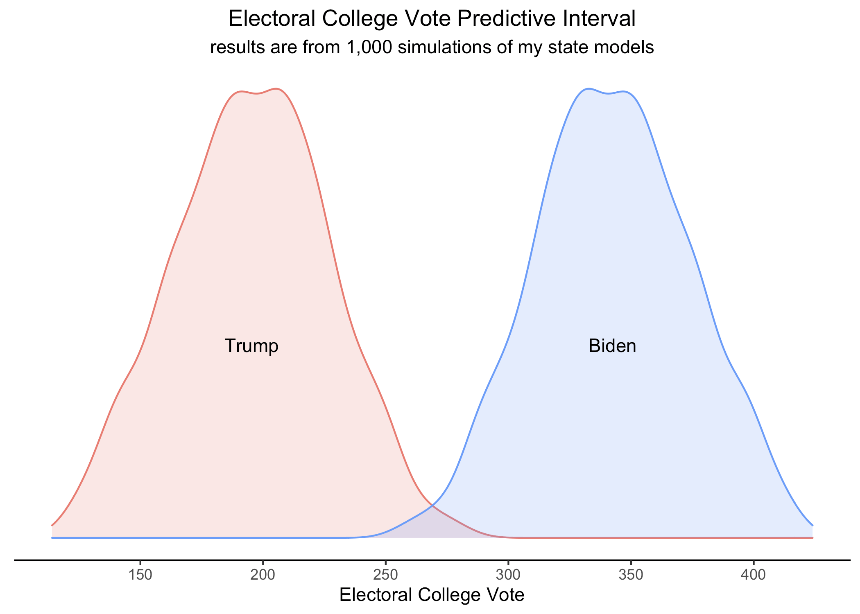
In my 1,000 simulations of the data, taking into account the fundamental uncertainty and also the standard error, Biden wins an average of 343 electoral votes in the simulations and Trump wins an average of 195 votes. In these simulated elections, Trump won a greater share of electoral college votes in 7 elections and there was an electoral college tie once. However, there are still many factors that this model does not take into account - such as the COVID-19 pandemic and the increased number of mail-in and early voting. These are uncertainties that no model can foresee, so we must be cautious as to not take these forecasts as truths. That being said, based only on these models, I expect to see Joe Biden winning the electoral college.