Social Dominance Theory

For some background information about Social Dominance Theory from Sidanius and Pratto (1999), their main idea was that human societies have the following group-based social hierarchies: an age hierarchy, a gender hierarchy, and possibly an arbitrary hierarchy system if a country is wealthy. Sidanius and Pratto also argue that the institutions within societies are either hierarchy enhancing (contributing to the hierarchy) or hierarchy attenuating (contributing to created social equality). In this blog, I explore data adapted from a Data for Progress and YouGov survey on registered voters that are representative of 2018 voters. This data includes a measure of SDO of each respondent and other political datapoints such as their party and who they voted for President in 2016.

Data Distribution

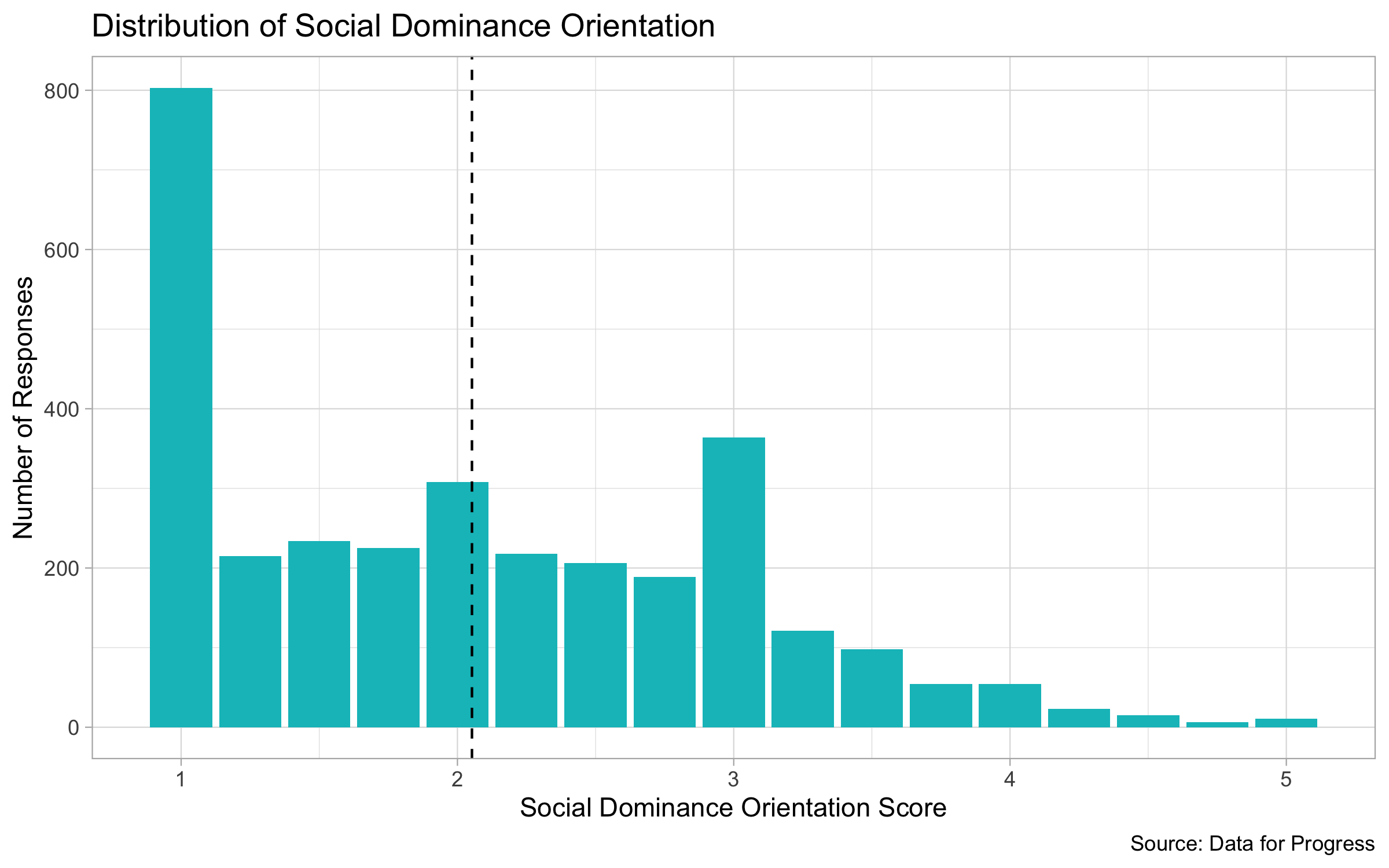
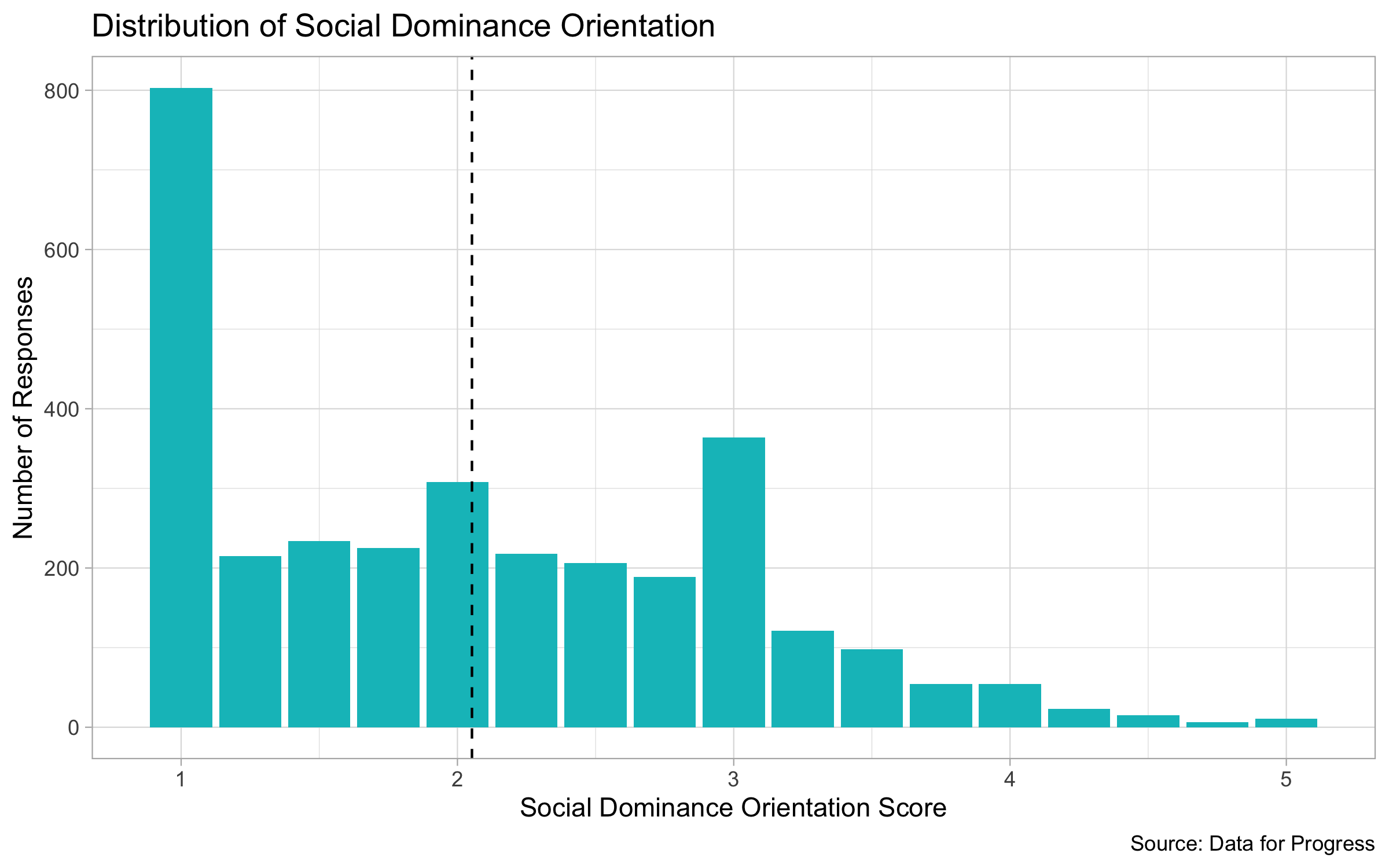
The overall distribution of SDO across the sample shows that there the distribution is right-skewed, so there are more respondents who had lower SDO scores and were less supportive of group-based hierarchies. Additionally, most respondents had the lowest SDO score of 1. The average score in the distribution is represented by the dotted line at about 2.1.

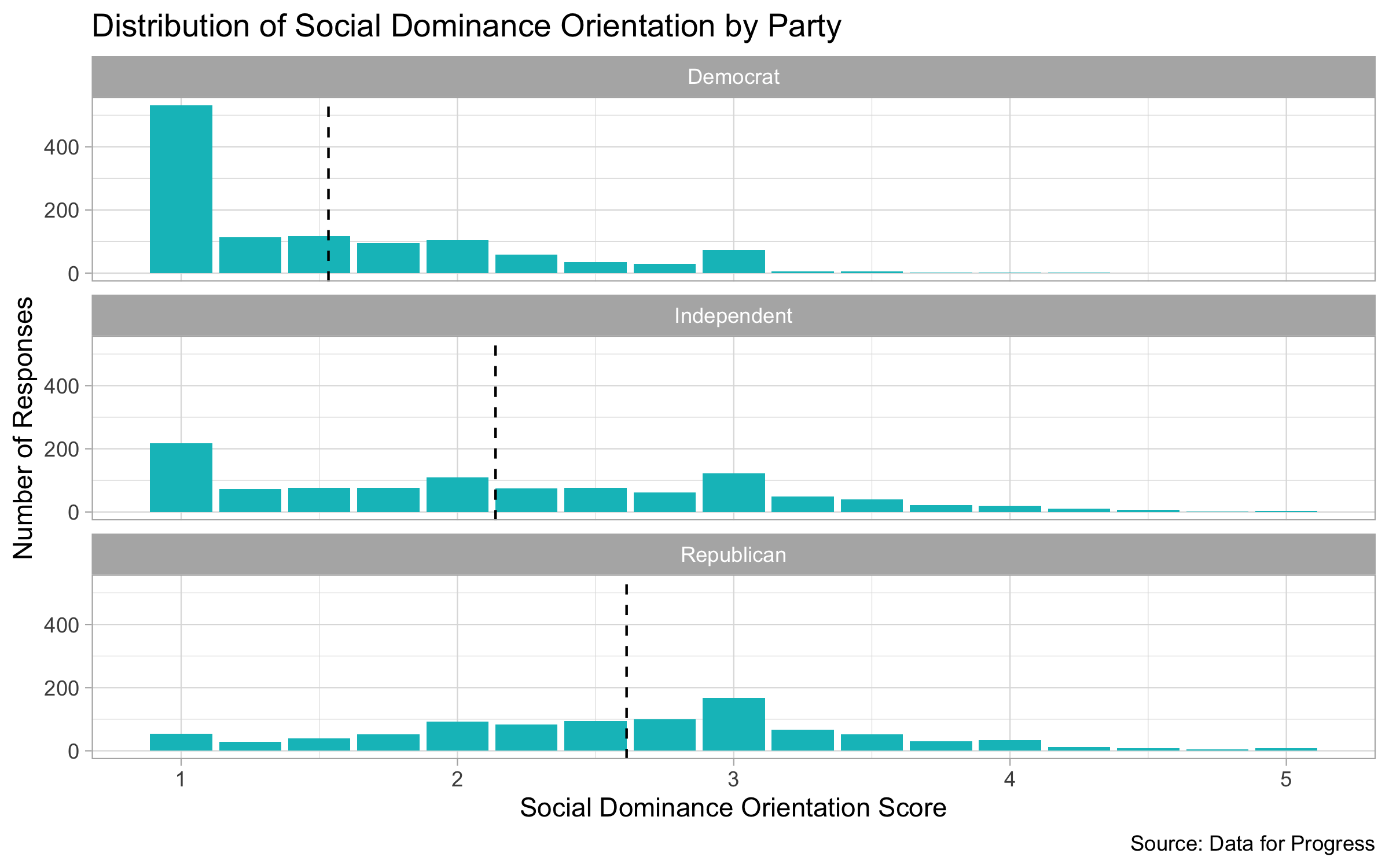
However, when we break down the distribution of SDO scores by party, we see a major shift from Democrats to Independents to Republicans. Democrats had on average the lowest SDO score of 1.6, Republicans had on average the highest SDO score of 2.6, and Independents were right in between with an average score of 2.2. We can also see that for Democrats and Independents, the most common score was 1, but for Republicans the most common score was 3.

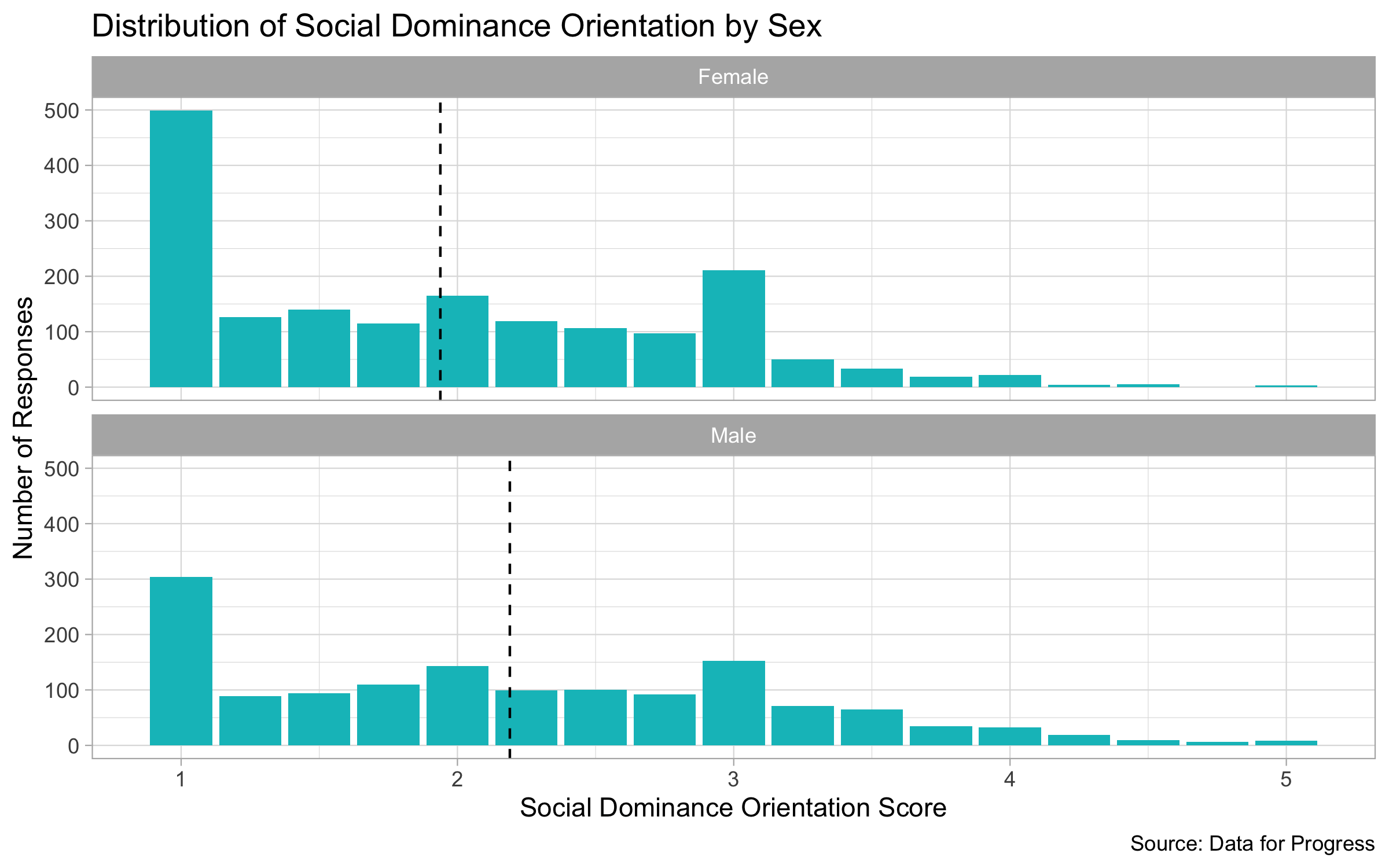
When breaking down the distribution by sex, we can also see a difference between male and female. Female respondents on average had an SDO score of 1.9 while male respondents on average had a score of 2.2. Both distributions were still left-skewed overall and had 1 as the most common score.

The distribution by party aligns with the thinking of Sidanius and Pratto (1999) because we know that older Americans are more likely to be more conservative and vote Republican and therefore have a higher SDO score by supporting an age hierarchy. This goes the same for the distribution by sex because there tends to be a patriarchal system in the United States so men would have higher SDO scores.

SDO as an explanatory variable

Thinking about how Republicans tend to have a higher SDO score on average in the sample and that older Americans and males are also more likely to have a higher SDO score, I also explore how SDO can be used as an explanatory variable or predictor in models such as one predicting which party an individual would vote for.

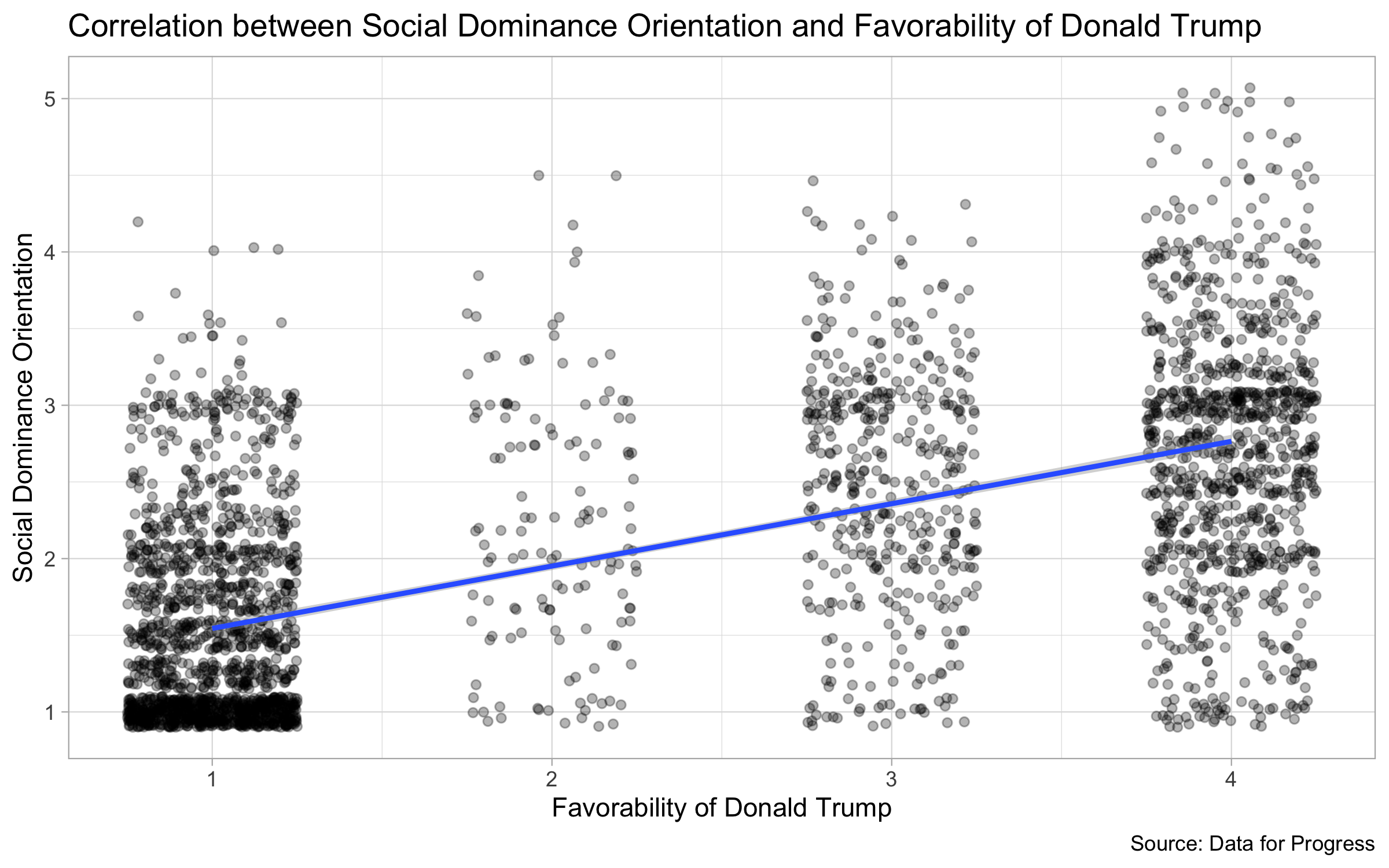
First, I evaluate the relationship between SDO score and favorability of Donald Trump. Unsurprisingly, we see a positive correlation that as ones’ SDO score increases, so does their favorability of Trump. However, how important is SDO as an explanatory variable if we already know that age and sex are also positively correlated with voting Republican and having a higher SDO score? I created the following model to test this:

\[ \begin{aligned} \text{rep_vote} = \beta_0 + \beta_1\text{sdo5} + \beta_2\text{female} + \beta_3\text{white} + \beta_4\text{educ} + \beta_5\text{age} + \beta_6\text{pid3} + \beta_7\text{ideo5} + \epsilon \end{aligned} \]

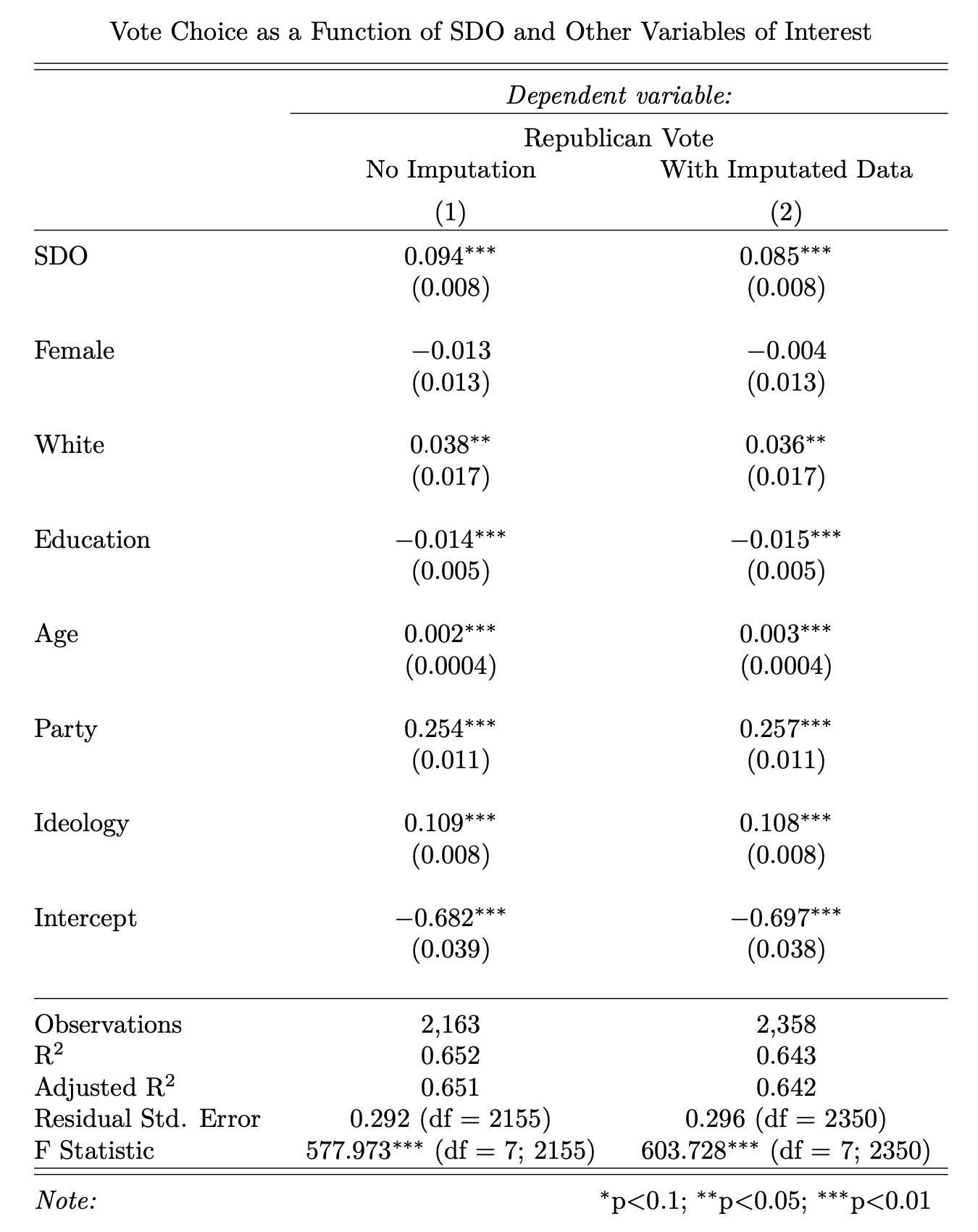
I tested the same model with two sets of data, one with the original data from the adapted dataset (1) and one with imputed values for the missing variables (2). Since there were not too many missing variables, the second model result in very similar outputs from the first model, so I will only focus on the first model here. The results show that even while controlling for sex, race, education, age, party, and ideology, SDO was still a statistically significant predictor for whether respondents in the data voted for a Republican in 2016 (Trump). An increase in SDO score by 1 predicts that the probability of a person voting Republican increases by about 0.094 on average.

Conclusion

So we know that SDO is an important measurement in politics, but how does this affect the world outside of academia? Well, we know that hierarchies play an important role in society and it has an effect on the way humans think. One might argue that hierarchies are bad for society and that they should be broken down so there is social equality. Others might argue that they are good for society because it motivates people to work hard to climb a social ladder. However, I disagree with both opinions. I don’t think the question should be if these hierarchies are good or bad. Instead, I think it’s just a natural aspect of how human societies developed. From debating the topic, creating policies related to it, or debating how the policies never can get past the partisan divide, it’s clear that this is another one of those “unfixable” aspects of the world. But once again it’s not unfixable if it’s not something that can be fixed to begin with. Hierarchies are just another natural part of our imperfect world.